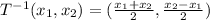Answer:
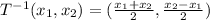
Explanation:
Given:
Linear transformation,
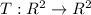 defined as
defined as
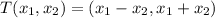
To Show: T is invertible
To find:
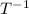
We know that Standard Basis of R² is
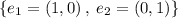
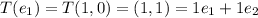
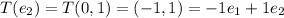
So, The matrix representation of T is

Now, Determinant of T = 1 - (-1) = 1 + 1 = 2 ≠ 0
⇒ Matrix Representation of T is Invertible matrix.
⇒ T is invertible Linear Transformation.
Hence Proved.
let,


Add (1) and (2),
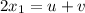
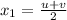
Putting this value in (1),
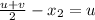
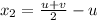
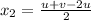
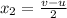
Now,
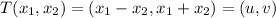
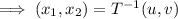
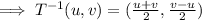
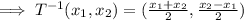
Therefore,