Question

How long will it take money to double if it is invested at 8​% compounded semiannually question mark 7.6 % compounded​ continuously?

Answer 1

Answer with explanation:

Let A be the Initial Amount.

Initial rate of Interest =8 %

Let , t = Time Period.

Since rate of Interest is compounded semiannually.

So, New rate of Interest = 4 %

New time period =2 t

Formula for Amount

`A=P* [1 +(R)/(100)]^n`

Present value of Money at 8​% compounded semiannually

`A=P * [ 1+(4)/(100)]^(2 t)`

-------------------------------------------------(1)

Let after ,Time period =h, the value of money doubles at 7.6 % compounded​ continuously.

`A=2P * [ 1+(7.6)/(100)]^(h)`

-------------------------------------------------(2)

Equating (1) and (2)

`\Rightarrow A * [ 1+(4)/(100)]^(2 t)=2A * [ 1+(7.6)/(100)]^(h)\\\\\Rightarrow (1.04)^(2 t)=2 * (1.076)^h`

where,t and h are integers.

Taking log on both sides

`\rightarrow 2 t \log (1.04)=\log 2 +h \log (1.076)\\\\ t=(\log 2 +h \log (1.076))/(2 \log (1.04))`

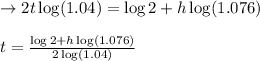
Replacing , t by y ,and h by x we get

`y=(\log 2 +x \log (1.076))/(2 \log (1.04))`

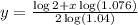
Substituting the values of log 2, log (1.076), and log (1.04) in the above equation

`y=(0.6932 +x * 0.07325)/(2 * 0.0393)\\\\ 0.786 y=0.6932+0.07325 x\\\\786 y=693.2 +73.25 x`

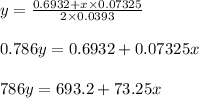
So, for distinct values of x we get distinct values of y.