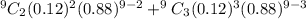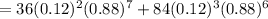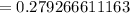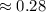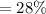Answer:
The probability is 28 % ( approx )
Explanation:
Since, there are only two possible outcomes in every trails ( residents are in their forties or not ),
So, this is a binomial distribution,
Binomial distribution formula,
Probability of success in x trials,
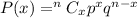
Where,
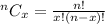
p and q are probability of success and failure respectively and n is the total number of trials.
Let X be the event of resident who are in his or her forties.
Here, p = 12% = 0.12,
⇒ q = 1 - p = 1 - 0.12 = 0.88,
n = 9,
Hence, the probability that two or three of the people in the group are in their forties = P(X=2) + P(X=3)