Answer:
a). There are 21 positive solutions and b). There are 45 solutions.
Explanation:
Given:
Equation, x + y + x = 8
To find: a). x, y, and z are all positive
b). x, y, and z are all non-negative
Here, Finding the number of solutions is equivalent to finding the number of ways to distribute 8 objects among 3 places.
a).
First let us given each place 1 object each.
Now, we find the number of ways to distribute 5 objects among three places.
Number of ways =
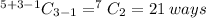
⇒ There are 21 positive solutions
b).
Here, we find the number of ways to distribute 8 objects among three places.
Number of ways =
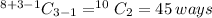
⇒ There are 45 negative solutions.
Therefore, a). There are 21 positive solutions and b). There are 45 solutions.