Question

What is the sum of the geometric sequence -4, 24, -144, if there are 6 terms

Answer 1

The sum is
`26,660`

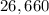
Explanation:

we know that

The formula of the sum in a geometric sequence is equal to

`S=a1[(1-r^(n))/(1-r)]`

where

a1 is the first term

r is the common ratio

n is the number of terms

we have

a1=-4, a2=24, a3=-144

Find the value of r (common ratio)

r=a2/a1

r=24/(-4)=-6

so

a1=-1

r=--6

n=6

substitute in the formula

`S=(-4)[(1-(-6)^(6))/(1-(-6))]`

`S=(-4)[(1-(-6)^(6))/(7)]`

`S=26,660`