Question

Let f: R --> R Prove that f is continuous on R iff f-1(H) is a closed set whenever H is a closed set

Answer 1

Answer with Step-by-step explanation:

We are given that a function is a continuous on R

f:R
`\rightarrow`R

We have to prove that if function is continuous ton R iff inverse image of closed set H is closed.

Let H be a closed set and function is continuous then R-H is a opens set

`f^(-1)(R-H)=f^(-1)(R)-f^(-1)(H)=R-f^(-1)(H)`=Open set

When function is continuous then inverse image of open set is open

Hence,
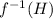`f^(-1)(H)`is a closed set

Conversely,

Let inverse image of closed set H is closed

If H is closed set then R-H is open set

`f^(-1)(R-H)=f^(-1)(R)-f^(-1)(H)=R-f^(-1)(H)`

When inverse image of closed set is closed then R-inverse image of H is opens set

When inverse image of open set is open then the function is continuous.

Hence, function is continuous.

Hence proved.