Answer with explanation:
It is given that:
f: R → R is a continuous function such that:
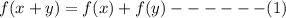 ∀ x,y ∈ R
∀ x,y ∈ R
Now, let us assume f(1)=k
Also,
( Since,
f(0)=f(0+0)
i.e.
f(0)=f(0)+f(0)
By using property (1)
Also,
f(0)=2f(0)
i.e.
2f(0)-f(0)=0
i.e.
f(0)=0 )
Also,
i.e.
f(2)=f(1)+f(1) ( By using property (1) )
i.e.
f(2)=2f(1)
i.e.
f(2)=2k
f(m)=f(1+1+1+...+1)
i.e.
f(m)=f(1)+f(1)+f(1)+.......+f(1) (m times)
i.e.
f(m)=mf(1)
i.e.
f(m)=mk
Now,
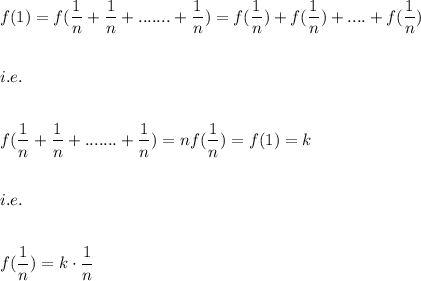
Also,
i.e.
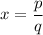
Then,

(
Now, as we know that:
Q is dense in R.
so Э x∈ Q' such that Э a seq
 belonging to Q such that:
belonging to Q such that:
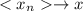 )
)
Now, we know that: Q'=R
This means that:
Э α ∈ R
such that Э sequence
 such that:
such that:
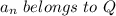
and

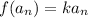
( since
 belongs to Q )
belongs to Q )
Let f is continuous at x=α
This means that:
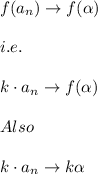
This means that:
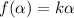
This means that:
f(x)=kx for every x∈ R