Question

$10000 is deposited in an account earning 4% interest compounded continuously. Use the continuous interest formula below to determine how long it takes for the amount in the account to double. Round answer to 2 decimal places. A = P e r t

_____years.

Answer 1

The required number of years are 7.52 years.

Explanation:

Given : $10000 is deposited in an account earning 4% interest compounded continuously.

To find : How long it takes for the amount in the account to double?

Solution :

Applying Continuous interest formula,

`A=Pe^(rt)`

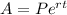
Where, P is the principal P=$10000

r is the interest rate r=4%=0.04

t is the time

We have given, Amount in the account to double

i.e. A=2P

Substitute the value in the formula,

`2P=Pe^(rt)`

`2=e^(0.04t)`

Taking log both side,

`\log 2=\log (e^(0.04t))`

`\log 2=0.04t* log e`

`t=(\log 2)/(0.04)`

`t=7.52`

Therefore, The required number of years are 7.52 years.