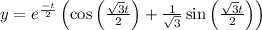Answer:
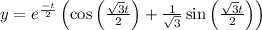
Explanation:
A second order linear , homogeneous ordinary differential equation has form
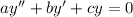 .
.
Given:
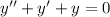
Let
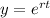 be it's solution.
be it's solution.
We get,
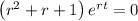
Since
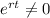 ,
,
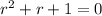
{ we know that for equation
 , roots are of form
, roots are of form
 }
}
We get,
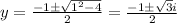
For two complex roots
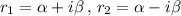 , the general solution is of form
, the general solution is of form
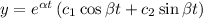
i.e

Applying conditions y(0)=1 on
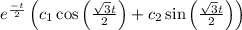 ,
,
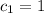
So, equation becomes
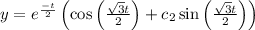
On differentiating with respect to t, we get
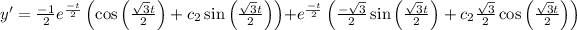
Applying condition: y'(0)=0, we get
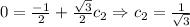
Therefore,