Answer:
3x+1.
Explanation:
First we divide g(x)/f(x) (the process is in the first image):
5x-15 in Z7[x] is 5x-1 and
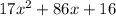 is
is
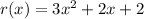 in Z7[x]. So
in Z7[x]. So
g(x)/f(x) =
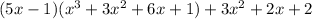
Now gcd(g,f) = gcm(f,r).
f(x)/r(x) =
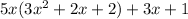
Then, gcd(f,r) = gcd(r,3x+1).
r/(3x+1) =
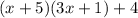
Then, gcd(r, 3x+1) = gcd(3x+1,4) = 3x+1.
So, gcd(f,g) = 3x+1.