Question

Use the Euclidean Algorithm to find the greatest common divisor of the polynomials f(x) = x^3 + 3x^2 + 6x + 1 and g(x) = 5x^4 + 2x^2 +x + 1 in Z7[x] .

Answer 1

3x+1.

Explanation:

First we divide g(x)/f(x) (the process is in the first image):

5x-15 in Z7[x] is 5x-1 and
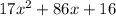`17x^2+86x+16` is
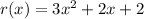`r(x)= 3x^2+2x+2` in Z7[x]. So

g(x)/f(x) =
`(5x-1)(x^3+3x^2+6x+1)+3x^2+2x+2`

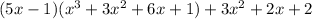
Now gcd(g,f) = gcm(f,r).

f(x)/r(x) =
`5x(3x^2+2x+2) + 3x+1`

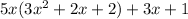
Then, gcd(f,r) = gcd(r,3x+1).

r/(3x+1) =
`(x+5)(3x+1) +4`

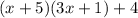
Then, gcd(r, 3x+1) = gcd(3x+1,4) = 3x+1.

So, gcd(f,g) = 3x+1.