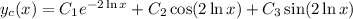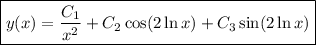Make the substitution
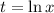 , then compute the derivatives of
, then compute the derivatives of
 with respect to
with respect to
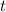 via the chain rule.
via the chain rule.
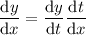
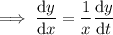
Let
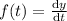 .
.
![(\mathrm d^2y)/(\mathrm dx^2)=(\mathrm d)/(\mathrm dx)\left[\frac fx\right]=(x(\mathrm df)/(\mathrm dx)-f)/(x^2)](https://img.qammunity.org/2020/formulas/mathematics/college/setkbry7hvvgv3gj4zl72vhhuafam1rjr4.png)
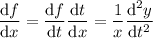
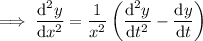
Let
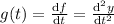 .
.
![(\mathrm d^3y)/(\mathrm dx^3)=(\mathrm d)/(\mathrm dx)\left[(g-f)/(x^2)\right]=(x^2\left((\mathrm dg)/(\mathrm dx)-(\mathrm df)/(\mathrm dx)\right)-2x(g-f))/(x^4)](https://img.qammunity.org/2020/formulas/mathematics/college/anbkgyphunzwiwl7yng57pli7ff5b393dd.png)
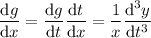
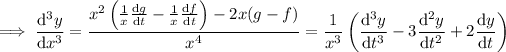
Substituting
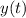 and its derivatives into the ODE gives a new one that is linear in
and its derivatives into the ODE gives a new one that is linear in
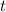 :
:
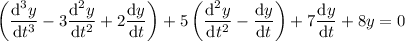
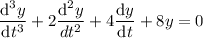
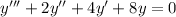
which has characteristic equation
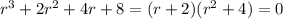
with roots
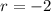 and
and
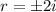 , so that the characteristic solution is
, so that the characteristic solution is
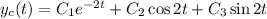
Replace
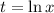 to solve for
to solve for
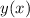 :
: