Answer:
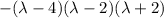
Explanation:
What we want to fator is:

There is no common factor, but let's factor it by grouping. The first two addends can be factor as follows:
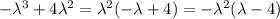
the second addends can be factor as well:
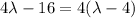 .
.
Then our original expression can be rewritten like
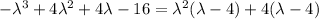
And here the
 is the common factor!
is the common factor!
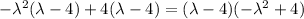
Finally, we can factor the quadratic expression as a difference of squares
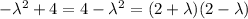
Ant we get
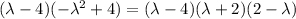
now, we can extract the negative sign from
 , and we get
, and we get
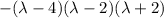 .
.