Question

Given that a(t) = 1/(t + 1)^2 represents the acceleration of a particle, find its velocity and position function which have conditions v(0) = 0 and x(0) = 1. Show your steps of integration well enough to demonstrate your understanding.

Answer 1

`v(t)=-(1)/(t+1) +1`

`x(t)=-ln(t+1)+t+1`

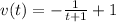
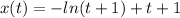
Explanation:

Integrate the function of the acceleration to find the function of the velocity

`v(t)=\int {(1)/((t+1)^2) } \, dt= \int {(t+1)^(-2)} \, dt =((t+1)^(-2+1))/(-2+1) +c_1\\v(t)=((t+1)^(-1))/(-1)+c_1 =-(1)/(t+1) +c_1`

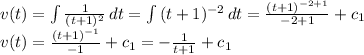
Use the initial condition
`v(0)=0` to find the value of the constant
`c_1`:

`v(0)=-(1)/((0)+1) +c_1=0\\-1 +c_1=0\\c_1=1\\\therefore v(t)=-(1)/(t+1) +1`

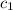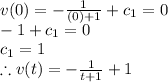
Integrate the function of the velocity to find the function of the position:

`x(t)=\int {-(1)/(t+1) +1} \, dt=-\int {(1)/(t+1) } \, dt+ \int {1} } \, dt\\x(t)=-ln(t+1)+t+c_2`

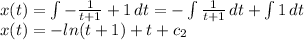
Use the initial condition
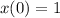`x(0)=1` to find the value of the constant
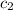`c_2`:

`x(0)=-ln(0+1)+0+c_2=1\\-ln(1)+c_2=1\\0+c_2=1\\c_2=1\\\therefore x(t)=-ln(t+1)+t+1`