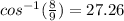Answer:
(-1,3,2)
Explanation:
For L1:
x= -1+2t
y= 3-t
z= 2+2t
and for L2:
x= -2-s
y= 5+2s
z=-2s
To find the intersection point we equalize the x, y and z:
-1+2t = -2-s
3-t = 5+2s
2+2t = -2s⇒ s= -1-t
We replace the s value -1-t in second equation:
3-t = 5+2(-1-t)
3-t = 5-2-2t
t = 0.
So, s = -1-t = -1-0 = -1.
We replace the s and t value in the parametric equations to find the interception point:
x= -1 +2(0) = -1
y = 3-0 = 3
z = 2 +2(0) = 2.
So, the interception point is (-1,3,2). The formula to calculate the angle is in the picture below, where α is the angle, u and v are the parallel vector of each line.
For L1: u=(2,-1,2) (the coefficients of t)
For L2: v=(-1,2,-2) (the coefficients of s)
So, the angle is:
cos(α) =

cos(α)=
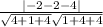
cos(α)=
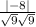
cos(α)=
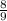
α =