Question

A medical research group plans to select 2 volunteers out of 8 for a drug experiment. In how many ways can they choose the 2 volunteers?

Answer 1

They can choose the 2 volunteers in 28 different ways

Explanation:

Well, as the research group has to choose 2 volunteers out of 8, this means that it doesn't matter the order in which they choose them as long as they are two.

In statistics this is considered a counting technique and is called combination.

The combination formula is:

`C(n,r)=(n!)/(r!(n-r)!)`

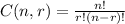
where

`n` is the set of elements

and

`r` is the number of elements taken from n

Then
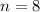`n=8` and
`r= 2`

We replace in the combination formula:

`C(8,2)=(8!)/(2!(8-2)!)`

`C(8,2)=(8!)/(2!(6!))`

`C(8,2)=(40320)/(2(720))`

`C(8,2)=(40320)/(1440)`

`C(8,2)=28}`

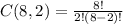
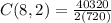
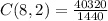
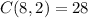
This result means that Medical research group can choose the 2 volunteers in 28 different ways