Question

Let O be the set of even integers. Define f : Z ? O by f(n) = 2n. Prove that f is a bijection in the following two different ways.

(a) Prove that f is both injective and surjective.

(b) Find an inverse g : O ? Z of f. (Show that g is an inverse of f.)

Answer 1

Check.

Explanation:

a. Let
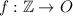`f: \mathbb{Z} \rightarrow O` such that f(n) = 2n.

Injective:

Let n, m
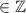`\in \mathbb{Z}` such that f(n)=f(m). Then,

2n = 2m and dividing both sides by 2 we obtain that n=m. Then f is injective.

Surjective:

Let n
`\in O`, so n = 2k for some integer k. Then, f(k) = n and therefore f is surjective.

b. Let
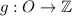`g: O \rightarrow \mathbb{Z}` such that g(n) = n/2. Then,

g(f(n)) = g(2n) = 2n/2 = n, and for m
`\in O`

f(g(m)) = f(m/2) = 2*m/2 = m.

Therefore, g is the inverse of f.