Answer:
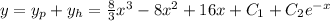
Explanation:
Let's find a particular solution. We need a function of the form
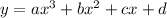 such that
such that
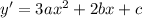 and
and
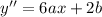
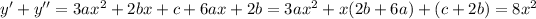
then, 3a= 8, 2b+6a =0 and c+2b = 0. With the first equation we obtain
a = 8/3 and replacing in the second equation 2b+6(8/3) = 2b + 16 = 0. Then, b = -8. Finally, c = -2(-8) = 16.
So, our particular solution is
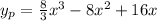 .
.
Now, let's find the solution
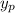 of the homogeneus equation
of the homogeneus equation
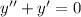 with the method of constants coefficients. Let
with the method of constants coefficients. Let
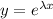
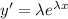
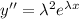
then
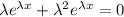
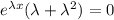

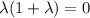
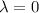 and
and
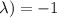 .
.
So,
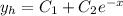 and the solution is
and the solution is
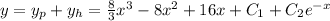 .
.