Answer:
4794.4 km/h
Step-by-step explanation:
Given:
The initial velocity v₁ = 4720 km/h
velocity of the motor,
 = 93 km/h (relative to the module)
= 93 km/h (relative to the module)
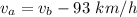
where,
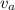 is the velocity of the motor
is the velocity of the motor
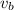 is the velocity of the command module
is the velocity of the command module
let, the mass of the command module be m
thus, the mass of the motor will be '4m'
Now. the mass of the vehicle before disengaged = 4m + m = 5m
using the concept conservation of momentum ,
we have
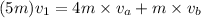
on substituting the values in the above equation, we get
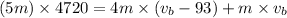
or
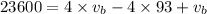
or
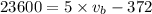
or
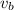 = 4794.4 km/h
= 4794.4 km/h