Question

You are working on a difficult passage from a new piece you are learning on the piano. If you have a probability of 2 out of 3 of playing it correctly on every attempt, and the attempts are independent(unfortunately!), what is the probability that you attempt to play it correctly 6 times when you try 8 times?

Answer 1

P=0.975%

Explanation:

You have a (2/3) probability of playing correctly each time that you make an attempt to play the passage, and that is independent of the number and results of the previous attempts. Be the probability 'p' the probability that you play the passage correctly in a single attempt.

`p=(2)/(3)`

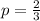
The probability that you play the passage correctly 2 times will be the multiplication of 'p' by itself, because, each attempt has its own contribution, so, analogously, The probability that you play the passage correctly 3 and 4 times would be
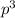`p^(3)` and
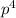`p^(4)` respectively. In the other hand, the probability 'p'' that you fail or play incorrectly the passage in a single attempt would be
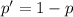`p'=1-p` because the total of possibilities for a single attempt are just two, to play correctly or not; so the total probability (which is 1) is
`1=p+p'`.

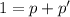The probability that you play incorrectly in a single attempt is

`p'=1-p=(1)/(3)`

The probability that you play incorrectly 3 times of three attempts would be the multiplication of p' 3 times by itself;

So, be P the probability that you play the passage correctly 6 times of 8. The probability would be:

`P={p^6}*{p'^2}`

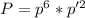
Because the event studied implies that you play correctly 6 times and incorrectly 2 times.

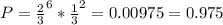`P={(2)/(3)}^6*{(1)/(3)}^2=0.00975=0.975` %