Question

A rock band is playing a concert at Music Hall 49, which has 2,500 seats. If 80% of the tickets were sold before the night of the concert, then there are how many tickets available on the the night of the concert?

250

500

750

1000

1250

Answer 1

First you must see how many seats were bought. To do this you must make a proportion

`(part)/(whole) = (part)/(whole)`

80 is a percent and percent's are always taken out of the 100. This means that one proportion will have 80 as the part and 100 as the whole

We want to know what 80% of 2,500 is in order to find how many seats were sold before the show. This means 2,500 is the whole and the unknown (let's make this x) is the part.

Here is your proportion:

`(x)/(2,500) =(80)/(100)`

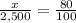
Now you must cross multiply

x*100 = 80*2,500

100x = 200,000

To isolate x divide 100 to both sides

100x/100 = 200,000/100

x = 2,000

This means that before the night of the concert 2,000 seats were bought.

We are still not done with this problem because we want to know how many seats are left the night of the concert. To find this simply subtract 2,000 from the number of original seating (2,500)

2,500 - 2,000 = 500

On the night of the concert there were 500 seats left.

Hope this helped!

~Just a girl in love with Shawn Mendes