Question

Give a counterexample to each claim:

(a) If x, y are both irrational then xy is also irrational

(b) For all n ? N, 2n 2 + 5 is prime

(c) For all a, b, n ? N, if n | ab then n | a or n | b.

Answer 1

a)
`x = √(2), \quad y = √(2)`

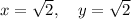
b) n = 5

c) n = 6, a = 4, b = 3

Explanation:

Incise a)

Let
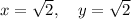`x = √(2), \quad y = √(2)`. Here
`√(2)` is a known irrational, and
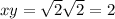`xy = √(2)√(2) = 2` where the number 2 is not only rational but integer.

Incise b)

If you take
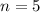`n = 5`, you will get 2(25) + 5 = 55 that is not prime, because 5 divides 55.

Incise c)

Here let n = 6, a = 4, b = 3. We can see that ab = 12, and of course 6 divides 12 (n | ab). But, also 6 does not divides 4 and 6 does not divides 3.