Question

If the sine of an angle equals to {2}/{5}, then the tangent of the angle could be:

1. sqrt(21)/2

2. 5/2

3. 2/sqrt(29)

4. sqrt(29)/2

5. 2/sqrt(21)

Answer 1

If the sine of an angle equals to {2}/{5}, then the tangent of the angle could be:

5.
`(2)/(√(21) )`

Explanation:

• Imagine a triangle

• The sine of an angle is equal to the length of the opposite leg over the hypotenuse.
• HINT: SOHCAHTOA

To find the adjacent leg (a):

Using the pythagorean theorem:
`a^(2) + b^(2) =c^(2)`

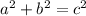
- a and b are the lenght of the sides and c is the hypotenuse

we know one side and the hypotenuse. Therefore plugging into the formula we get:

`a^(2) + 2^(2) =5^(2)`

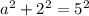
where a is the adjacent leg of the triangle, solving for a we get:

`a^(2) =5^(2)- 2^(2)`

`a^(2) = 21`

`a = √(21)`

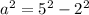
To find the tangent of the angle:

Since tangent is opposite leg over the adjacent leg:

tan θ =
`(2)/(√(21) )`