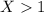Answer:
1. X > 1
Explanation:
We know
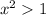 because
because
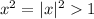 . That's why
. That's why
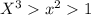 .
.
We can now subtract 1 in both sides of the inequality:
 .
.
Factoring
 as a difference of cubes, we get:
as a difference of cubes, we get:
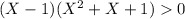 .
.
Thus, we have two factors whose multiplication is positive. Then, both are positive or both are negative. The second case is impossible, because
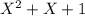 can never be positive. The reason is the following:
can never be positive. The reason is the following:
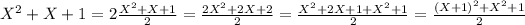
witch is always positive because
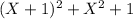 is a sum of squares, and the squares are always positive.
is a sum of squares, and the squares are always positive.
We conclude that both
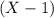 and
and
 have to be positive, and then
have to be positive, and then
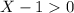 implies
implies