Question

Please help solve these proofs asap!!!

Answer 1

Proofs contained within the explanation.

Explanation:

These induction proofs will consist of a base case, assumption of the equation holding for a certain unknown natural number, and then proving it is true for the next natural number.

a)

Proof

Base case:

We want to shown the given equation is true for n=1:

The first term on left is 2 so when n=1 the sum of the left is 2.

Now what do we get for the right when n=1:

`(1)/(2)(1)(3(1)+1)`

`(1)/(2)(3+1)`

`(1)/(2)(4)`

`2`

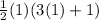
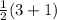
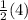
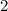
So the equation holds for n=1 since this leads to the true equation 2=2:

We are going to assume the following equation holds for some integer k greater than or equal to 1:

`2+5+8+\cdots+(3k-1)=(1)/(2)k(3k+1)`

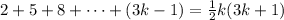
Given this assumption we want to show the following:

`2+5+8+\cdots+(3(k+1)-1)=(1)/(2)(k+1)(3(k+1)+1)`

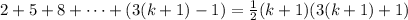
Let's start with the left hand side:

`2+5+8+\cdots+(3(k+1)-1)`

`2+5+8+\cdots+(3k-1)+(3(k+1)-1)`

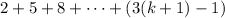
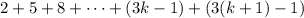
The first k terms we know have a sum of .5k(3k+1) by our assumption.

`(1)/(2)k(3k+1)+(3(k+1)-1)`

Distribute for the second term:

`(1)/(2)k(3k+1)+(3k+3-1)`

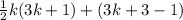
Combine terms in second term:

`(1)/(2)k(3k+1)+(3k+2)`

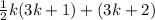
Factor out a half from both terms:

`(1)/(2)[k(3k+1)+2(3k+2]`

Distribute for both first and second term in the [ ].

`(1)/(2)[3k^2+k+6k+4]`

Combine like terms in the [ ].

`(1)/(2)[3k^2+7k+4`

The thing inside the [ ] is called a quadratic expression. It has a coefficient of 3 so we need to find two numbers that multiply to be ac (3*4) and add up to be b (7).

Those numbers would be 3 and 4 since

3(4)=12 and 3+4=7.

So we are going to factor by grouping now after substituting 7k for 3k+4k:

`(1)/(2)[3k^2+3k+4k+4]`

`(1)/(2)[3k(k+1)+4(k+1)]`

`(1)/(2)[(k+1)(3k+4)]`

`(1)/(2)(k+1)(3k+4)`

`(1)/(2)(k+1)(3(k+1)+1)`.

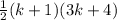
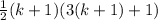Therefore for all integers n equal or greater than 1 the following equation holds:

`2+5+8+\cdots+(3n-1)=(1)/(2)n(3n+1)`

//

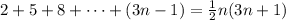
b)

Proof:

Base case: When n=1, the left hand side is 1.

The right hand at n=1 gives us:

`(1)/(4)(5^1-1)`

`(1)/(4)(5-1)`

`(1)/(4)(4)`

`1`

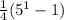
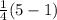
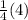
So both sides are 1 for n=1, therefore the equation holds for the base case, n=1.

We want to assume the following equation holds for some natural k:

`1+5+5^2+\cdots+5^(k-1)=(1)/(4)(5^k-1)`.

We are going to use this assumption to show the following:

`1+5+5^2+\cdots+5^((k+1)-1)=(1)/(4)(5^(k+1)-1)`

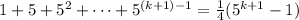
Let's start with the left side:

`1+5+5^2+\cdots+5^((k+1)-1)`

`1+5+5^2+\cdots+5^(k-1)+5^((k+1)-1)`

We know the sum of the first k terms is 1/4(5^k-1) given by our assumption:

`(1)/(4)(5^k-1)+5^((k+1)-1)`

`(1)/(4)(5^k-1)+5^k`

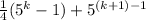
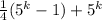
Factor out the 1/4 from both of the two terms:

`(1)/(4)[(5^k-1)+4(5^k)]`

`(1)/(4)[5^k-1+4\cdot5^k]`

Combine the like terms inside the [ ]:

`(1)/(4)(5 \cdot 5^k-1)`

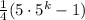
Apply law of exponents:

`(1)/(4)(5^(k+1)-1)`

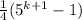
Therefore the following equation holds for all natural n:

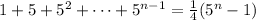`1+5+5^2+\cdots+5^(n-1)=(1)/(4)(5^n-1)`.

//