Question

Find the integral of ((x^(2)-1))/(x^(2)+3x) using integration by partial fractions

Answer 1

`x+(-1)/(3) \ln|x|+(-8)/(3)\ln|x+3|+C`

Explanation:

To use partial fractions, I'm going to first do long division because the degree of the top is more than or equal to that of the bottom.

After I have that the degree of the bottom is more than the degree of the top, I will factor my bottom to figure out what kinds of partial fractions I'm going to have.

Let's begin with the long division:

The bottom goes outside.

The top goes inside.

1

-----------------

x^2+3x| x^2 -1

-(x^2+3x)

-----------------------------

-3x -1

We can not going any further since the divisor is more in degree than the left over part.

So we have so for that the integrand given equals:

`(x^2-1)/(x^2+3x)=1+(-3x-1)/(x^2+3x)`

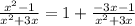
The 1 will of course not need partial fraction.

So we know our answer is x + something + C

Since the derivative of (x+c)=(1+0)=1.

Let's focus now on:

`(-3x-1)/(x^2+3x)`

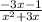
The bottom is not too bad too factor because it is binomial quadratic containing terms with a common factor of x:

`x^2+3x=x(x+3)`

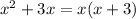
Since both factors our linear and there are two factors, then we will have two partial fractions where the numerators are both constants.

So we are looking to make this true:

`(-3x-1)/(x^2+3x)=(A)/(x)+(B)/(x+3)`

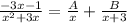
Some people like to combine the fractions on the left and then regroup the terms and then compare coefficients.

Some people also prefer a method called heaviside method.

So I'm actually going to do this last way and I will explain it as I got.

We are going to clear the fractions by multiplying both sides by
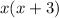`x(x+3)` giving me:

`-3x-1=A(x+3)+Bx`

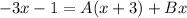
I know x+3 will be 0 when x=-3 so entering in -3 for x gives:

`-3(-3)-1=A(-3+3)+B(-3)`

`9-1=A(0)-3B`

`8=-3B`

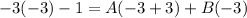
Divide both sides by -3:

`(8)/(-3)=B`

`B=(-8)/(3)`/

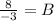
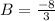Now let's find A. If I replace x with 0 then Bx becomes 0 giving me:

`-3(0)-1=A(0+3)+B(0)`

`-1=A(3)+0`

`-1=3A`

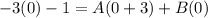
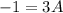
Divide both sides by 3:

`(1)/(-3)=A`

`(-1)/(3)=A`

Okay let me also who you other method of just comparing coefficients.

`-3x-1=A(x+3)+Bx`

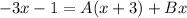
Distribute on the right:

`-3x-1=Ax+3A+Bx`

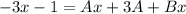
Regroup terms on right so like terms are together:

`-3x-1=(A+B)x+3A`

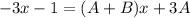
Now if this is to be true then we need:

-3=A+B and -1=3A

The second equation can be solved by dividing both sides by 3 giving us:

-3=A+B and -1/3=A

Now we are going to plug that second equation into the first:

-3=A+B with A=-1/3

-3=(-1/3)+B

Add 1/3 on both sides:

-3+(-1/3)=B

-8/3=B

So either way you should get the same A and B if no mistake is made of course.

So this is the integral we are looking at now (I'm going to go ahead and include the 1 from earlier):

`\int (1+((-1)/(3))/(x)+((-8)/(3))/(x+3))dx`

`x+(-1)/(3) \ln|x|+(-8)/(3)\ln|x+3|+C`

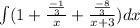
Why I did choose natural log for both of those 2 terms' antiderivatives?

Because they are a constant over a linear expression. Luckily both of those linear expressions had a leading coefficient of 1.

Also recall the derivative of ln(x) is (x)'/x=1/x and

the derivative of ln(x+3) is (x+3)'/(x+3)=(1+0)/(x+3)=1/(x+3).

Let's check our answer:

To do that we need to differentiate what we have for the integral and see if we wind up with the integrand.

`(d)/(dx)(x+(-1)/(3) \ln|x|+(-8)/(3)\ln|x+3|+C)`

`1+(-1)/(3) (1)/(x)+(-8)/(3)(1)/(x+3)+0`

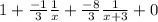
We are going to find a common denominator which would be the least common multiple of the denominators which is x(x+3):

`(x(x+3)+(-1)/(3)(x+3)+(-8)/(3)(x))/(x(x+3))`

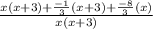
Now distribute property:

`(x^2+3x+(-1)/(3)x-1+(-8)/(3)x)/(x^2+3x)`

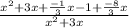
Combine like terms:

`(x^2+3x+(-9)/(3)x-1)/(x^2+3x)`

`(x^2+3x-3x-1)/(x^2+3x)`

`(x^2-1)/(x^2+3x)`

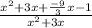
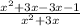
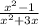
So that is the same integrand we started with so our answer has been confirmed.