Question

Ciara is swinging a 0.015 kg ball tied to a string around her head in a flat, horizontal circle. The radius of the circle is 0.70 m. It takes the ball 0.60 seconds to complete one full circle. Calculate the tension in the string and its direction that provides the centripetal force acting on the ball to keep it in the circular path.

A) 0.0077 N, toward the center of the circle
B) 1.2 N, toward the center of the circle
C) 0.0077 N, along the line tangent to the circle
D) 1.2 N, along the line tangent to the circle

Answer 1

B) 1.2 N, toward the center of the circle

Step-by-step explanation:

The circumference of the circle is:

C = 2πr

C = 2π (0.70 m)

C = 4.40 m

So the velocity of the ball is:

v = C/t

v = 4.40 m / 0.60 s

v = 7.33 m/s

Sum of the forces in the radial direction:

∑F = ma

T = m v² / r

T = (0.015 kg) (7.33 m/s)² / (0.70 m)

T = 1.2 N

The tension force is 1.2 N towards the center of the circle.

Answer 2

1.2 N, toward the center of the circle

Step-by-step explanation:

It is given that,

Mass of the ball, m = 0.015 kg

The radius of the circle, r = 0.7 m

Time taken by the ball to complete complete circle, t = 0.6 s

We need to find the tension in the string and its direction that provides the centripetal force acting on the ball to keep it in the circular path. Here, tension in the string balances the centripetal force so that the ball moves in circular path. So,

`T=(mv^2)/(r)`

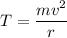
Since,
`v=(2\pi r)/(t)=(2\pi * 0.7)/(0.6)=7.33\ m/s`

So,
`T=(0.015* (7.33)^2)/(0.7)`

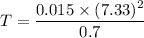
T = 1.15 N

or

T = 1.2 N

The direction of centripetal force is toward the center of circle. So, the correct option is (b).