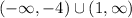Answer:
So any number in the following set is a solution:
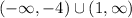
given the inequality to solve was:
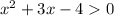
Explanation:
The left hand side is a quadratic while the right hand side is 0.
Since this is a quadratic>0, I'm going to factor the quadratic if possible and then solve that quadratic=0 for x.
That is I'm going to solve:
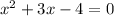
Since a=1, I get to ask what multiplies to be c (-4) and add up to be b(3).
Those numbers are 4 and -1.
So the factored form for the equation is:
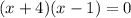
Setting both factors equal to 0 since 0*anything=0:
x+4=0 and x-1=0
-4 -4 +1 +1
---------------------------------------------------
x=-4 and x=1
Ok so if this wasn't a quadratic I would make a number line and choose numbers to plug into the quadratic to see which intervals would give me positive results. I say positive due to the >0 part.
However since I know about the shapes of quadratics, I'm going to use that.
The quadratic function
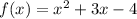 has x-intercepts (-4,0) and (1,0) and is open up.
has x-intercepts (-4,0) and (1,0) and is open up.
I determine that it was opened up because the leading coefficient is 1 which is positive.
Now the left tail and right tail is what is above the x-axis so the solution set is: