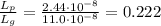Question

Two wires have the same resistance and diameter. If the wires are made of platinum and gold with resistivities respectively of 11.0 ✕ 10−8 Ω · m and 2.44 ✕ 10−8 Ω · m, determine the ratio of their lengths.

Answer 1

0.222

Step-by-step explanation:

The resistance of a wire is given by

`R=\rho (L)/(A)`

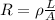
where

`\rho` is the resistivity

L is the length of the wire

A is the cross-sectional area

Here let's call
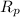`R_p` the resistance of the platinum wire and
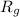`R_g` the resistance of the gold wire. The two resistances are equal, so we can write

`R_p = R_g`

`\rho_P (L_p)/(A_p)=\rho_g (L_g)/(A_g)`

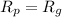
Where

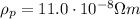`\rho_p = 11.0\cdot 10^(-8) \Omega m` is the resistivity of platinum

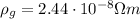`\rho_g = 2.44\cdot 10^(-8)\Omega m` is the resistivity of gold

We know that the two wires also have same diameter, so same cross-sectional area, so

`A_p = A_g`

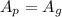
Therefore we can rewrite the equation as

`(L_p)/(L_g)=(\rho_g)/(\rho_p)`

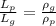
And so the ratio of the lengths of the two wires is

`(L_p)/(L_g)=(2.44\cdot 10^(-8))/(11.0\cdot 10^(-8))=0.222`