Question

In an interstellar gas cloud at 42.6 K, the pressure is 1.06 x 10-8 Pa. Assuming that the molecular diameters of the gases in the cloud are all 19.2 nm, what is their mean free path?

Answer 1

Answer : The mean free path is, 33.88 m

Explanation :

First we have to calculate the volume of for mole of gas by using ideal gas equation.

`PV=nRT`

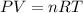
where,

P = pressure of gas =
`1.06* 10^(-8)Pa`

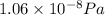
V = volume of gas = ?

T = temperature of gas = 42.6 K

n = number of moles of gas = 1 mole

R = gas constant =
`8.314Pa.m^3/mole.K`

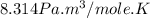
Now put all the given values in the ideal gas equation, we get:

`(1.06* 10^(-8)Pa)* (V)=1mole* (8.314Pa.m^3/mole.K)* (42.6K)`

`V=3.34* 10^(10)m^3`

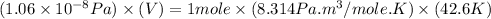
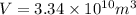
Now we have to calculate the number of molecules per unit volume.

`(N)/(V)=(n* N_A)/(V)=((1mole)* (6.022* 10^(23)))/(3.34* 10^(10)m^3)=1.803* 10^(13)molecule/m^3`

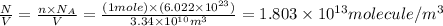
Now we have to calculate the mean free path.

Formula used :

`\text{Mean free path}=(1)/(√(2)\pi d^2((N)/(V)))`

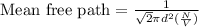
where,

d = diameter pf molecule =
`19.2nm=19.2* 10^(-9)m`

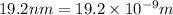
conversion used :
`1nm=10^(-9)m`

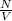`(N)/(V)` = number of molecules per unit volume

Now put all the given values in this formula, we get:

`\text{Mean free path}=(1)/(√(2)* (3.14) (19.2* 10^(-9))^2* (1.803* 10^(13)))`

`\text{Mean free path}=33.88m`

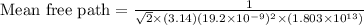
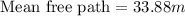
Therefore, the mean free path is, 33.88 m