Question

A game has an expected value to you of ​$600. It costs ​$600 to​ play, but if you​ win, you receive​ $100,000 (including your ​$600 ​bet) for a net gain of ​$99 comma 400. What is the probability of​ winning?

Answer 1

Given:

Expected value, E(X)= $600

Net Profit = $99400

Cost of playing once = $600

Solution:

Let the probability of winning be P(X) and that of losing
`P(\bar{X})`

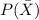
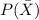`P(\bar{X})` = 1 - P(X)

Now expected value, E(X) =
`Profit* P(X) + loss*P(\bar{X})`

E(X) = 99400P(X) + (-400)(1 - P(X))

600 = 99400P(X) -400 +400P(X)

P(X) = 0.01

Therefore, the probability of winning is P(X) = 0.01 or 1%