Answer:
The room is 996.13 ft by 889.13 ft
Step-by-step explanation:
let AC = x
AB = 77+x
BC = 1313
Therefore using Pythagoras theorem, we get
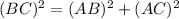
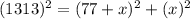

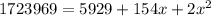
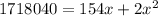
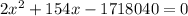
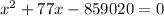
Therefore on solving, we get
x = 889.13 ft
∴ The dimension of the rectangular room is
AC = x = 889.13 ft
AB = 77+x = 77+ 889.13 = 996.13 ft
Therefore the room is 996.13 ft by 889.13 ft