Answer:
The length of the smaller diagonal is d_1 = 6.44 units
The length of the longer diagonal is d_2 = 15.77 units
Step-by-step explanation:
Given: A parallelogram has sides of lengths 9 and 8, and one angle is 44°.
We can use the cosine formula to find the measures of the diagonals.
The cosine formula is
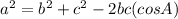
We can divide the parallelogram into two equal triangles.
Triangle 1
Which has the two sides measures 9 and 8 and including angle is 44°.
If we are given two sides and one angle, we can use the cosine formula and find the third side. Here third side is diagonal 1.
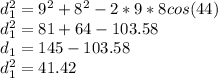
Taking square root on both sides, we get
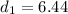 [Rounded to the nearest hundredths place]
[Rounded to the nearest hundredths place]
Triangle 2
It is a parallelogram, the opposite sides are equal. Therefore, the another triangle has equal measures but angle differs.
The adjacent angles in a parallelogram add upto 180°.
Therefore, the angle measure is 180 - 44 = 136°.
Now let's use the cosine formula and find the measure diagonal 2.
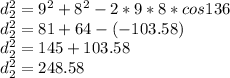
Taking the square root on both sides, we get
 [Rounded to the nearest hundredths place]
[Rounded to the nearest hundredths place]
So the length of the smaller diagonal is d_1 = 6.44 units
the length of the longer diagonal is d_2 = 15.77 units