Question

A monopolist earns $60 million annually and will maintain that level of profit indefinitely, provided that no other firm enters the market. However, if another firm enters the market, the monopolist will earn $60 million in the current period and $20 million annually thereafter. The opportunity cost of funds is 18 percent, and profits in each period are realized at the beginning of each period.

a. What is the present value of the monopolist’s current and future earnings if entry occurs?b. If the monopolist can earn $35 million indefinitely by limit pricing, should it do so? Explain.

Answer 1

Given:

Monopolist earns = $60 million

The opportunity cost of funds = 18 %

The monopolist will earn = $20 million after another firm enters the market

The present value of the monopolist’s current and future earnings if entry occurs can be computed using the following formula:

`\Pi_(MD) = Earning Annualy + (Earning After firm enters)/(Opportunity cost)`

`\Pi_(MD) = \Pi_(M) + (\Pi_(D))/(i)`

`\Pi_(MD) = 60 + (20)/(0.18)`

`\Pi_(MD) = 171.1`

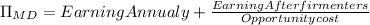
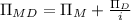
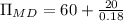
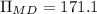
The present value of the monopolist’s is $171.1 million

If the monopolist can earn $35 million indefinitely by limit pricing,then the present value of the monopolist’s current earnings:

`\Pi_(MD) = \Pi_(M) + (\Pi_(D))/(i)`

`\Pi_(MD) = 60 + (35)/(0.18)`

`\Pi_(MD) = 254.4`

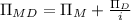
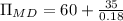
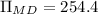
∴ If the monopolist can earn $35 million indefinitely by limit pricing, then they should do so.