Question

A horizontal block-spring system with the block on a frictionless surface has total mechanical energy E = 50.9 J and a maximum displacement from equilibrium of 0.204 m. (a) What is the spring constant? N/m (b) What is the kinetic energy of the system at the equilibrium point? J (c) If the maximum speed of the block is 3.45 m/s, what is its mass? kg (d) What is the speed of the block when its displacement is 0.160 m? m/s (e) Find the kinetic energy of the block at x = 0.160 m. J (f) Find the potential energy stored in the spring when x = 0.160 m. J (g) Suppose the same system is released from rest at x = 0.204 m on a rough surface so that it loses 12.2 J by the time it reaches its first turning point (after passing equilibrium at x = 0). What is its position at that instant? m

Answer 1

(a) 2446 N/m

When the spring is at its maximum displacement, the elastic potential energy of the system is equal to the total mechanical energy:

`E=U=(1)/(2)kA^2`

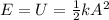
where

U is the elastic potential energy

k is the spring constant

A is the maximum displacement (the amplitude)

Here we have

U = E = 50.9 J

A = 0.204 m

Substituting and solving the formula for k,

`k=(2E)/(A^2)=(2(50.9))/((0.204)^2)=2446 N/m`

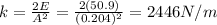
(b) 50.9 J

The total mechanical energy of the system at any time during the motion is given by:

E = K + U

where

K is the kinetic energy

U is the elastic potential energy

We know that the total mechanical energy is constant: E = 50.9 J

We also know that at the equilibrium point, the elastic potential energy is zero:

`U=(1)/(2)kx^2=0` because x (the displacement) is zero

Therefore the kinetic energy at the equilibrium point is simply equal to the total mechanical energy:

`K=E=50.9 J`

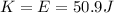
(c) 8.55 kg

The maximum speed of the block is v = 3.45 m/s, and it occurs when the kinetic energy is maximum, so when

K = 50.9 J (at the equilibrium position)

Kinetic energy can be written as

`K=(1)/(2)mv^2`

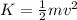
where m is the mass

Solving the equation for m, we find the mass:

`m=(2K)/(v^2)=(2(50.9))/((3.45)^2)=8.55 kg`

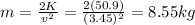
(d) 2.14 m/s

When the displacement is

x = 0.160 m

The elastic potential energy is

`U=(1)/(2)kx^2=(1)/(2)(2446)(0.160)^2=31.3 J`

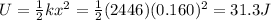
So the kinetic energy is

`K=E-U=50.9 J-31.3 J=19.6 J`

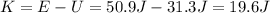
And so we can find the speed through the formula of the kinetic energy:

`K=(1)/(2)mv^2 \rightarrow v=\sqrt{(2K)/(m)}=\sqrt{(2(19.6))/(8.55)}=2.14 m/s`

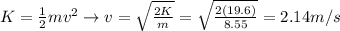
(e) 19.6 J

The elastic potential energy when the displacement is x = 0.160 m is given by

`U=(1)/(2)kx^2=(1)/(2)(2446)(0.160)^2=31.3 J`

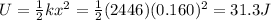
And since the total mechanical energy E is constant:

E = 50.9 J

the kinetic energy of the block at this point is

`K=E-U=50.9 J-31.3 J=19.6 J`

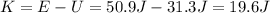
(f) 31.3 J

The elastic potential energy stored in the spring at any time is

`U=(1)/(2)kx^2`

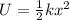
where

k = 2446 N/m is the spring constant

x is the displacement

Substituting

x = 0.160 m

we find the elastic potential energy:

`U=(1)/(2)kx^2=(1)/(2)(2446)(0.160)^2=31.3 J`

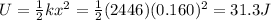
(g) x = 0

The postion at that instant is x = 0, since it is given that at that instant the system passes the equilibrium position, which is zero.