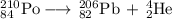Answer:
Step-by-step explanation:
Your unbalanced nuclear equation is:
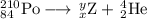
The main point to remember in balancing nuclear equations is that the sums of the superscripts and the subscripts must be the same on each side of the equation.
Then
84 = x + 2, so x = 84 - 2 = 82
210 = y + 4, so y = 210 - 4 = 206
Element 82 is lead, so the nuclear equation becomes