Question

Use the arc length formula to find the length of the curve y = 4x − 5, −1 ≤ x ≤ 3. Check your answer by noting that the curve is a line segment and calculating its length by the distance formula.

Answer 1

`4√(17)`

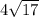
Explanation:

Let's find the answer by using the arc length formula which is:

`\int\limits^a_b {\sqrt{1+((dy)/(dx))^(2) } } \, dx`

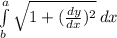
First, let's find dy/dx which is:

y=4x-5

y'=4*(1)-0

y'=4, now let's use the formula:

`\int\limits^3_(-1) {\sqrt{1+4^(2)} } \, dx=√(17) *(3-(-1))=4√(17)`

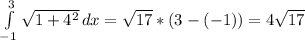
Now, using the distance formula we have:

`d=\sqrt{(x2-x1)^(2) +(y2-y1)^(2) }`

`y(-1)=4*(-1)-5=-9 \\y(3)=4*(3)-5=7`

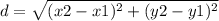
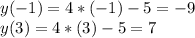
So we have two points (-1, -9) and (3, 7) so:

`d=\sqrt{(3-(-1))^(2) +(7-(-9))^(2) }=4√(17)`

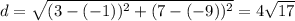
Notice both equations gave the same length
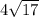`4√(17)`.