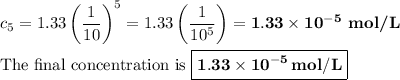Answer:
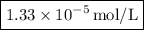
Step-by-step explanation:
Data:
c₀ = 1.33 mol·L⁻¹
Dilutions = 2 mL stock + 18 mL water
n = five dilutions
Calculations:
The general formula is for calculating a single dilution ratio (DR) is
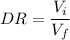
For your dilutions,
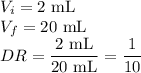
(Note: This is the same as a dilution factor of 10:1)
The general formula for the concentration cₙ after n identical serial dilutions is
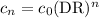
So, after five dilutions