Question

Integrate x^2/4-x^3​dx

Answer 1

`(-1)/(3) \ln|4-x^3|+C` is the answer

if
`\int (x^2 dx)/(4-x^3)` or
`\int (x^2)/(4-x^3) dx` was the integral.

Explanation:

`\int (x^2 dx)/(4-x^3)`.

I know the derivative of
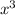`x^3` will give me
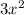`3x^2` and I see the variable part of this in the numerator.

So my subsitution will be
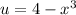`u=4-x^3` and differentiating both sides gives:

`(du)/(dx)=0-3x^2`

`du=-3x^2 dx`

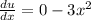
I'm going to solve for
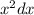`x^2 dx` since that is my numerator.

Divide both sides by -3:

`(-1)/(3)du=x^2 dx`

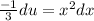
Inputting my substitution with it's derivative into the integral gives me:

`\int (x^2 )/(4-x^3)dx=int (x^2 dx)/(4-x^3)`

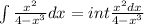
with
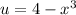`u=4-x^3` and
`(-1)/(3)du=x^2 dx`:

`\int (-1)/(3) du}{u}`

`(-1)/(3) \int (du)/(u)`

`(-1)/(3) \int u^(-1) du`

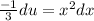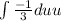
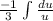
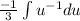
Don't use power rule.

`(-1)/(3) \ln|u|+C`

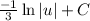
Put back in terms of x:

`(-1)/(3) \ln|4-x^3|+C`

Let's check our answer by differentiating it:

`(-1)/(3)(\ln|4-x^3|)'`

`(-1)/(3) \cdot (-3x^2)/(4-x^3)`

`(x^2)/(4-x^3)`

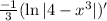
We are good. Our check it worked out.