Answer:
a)
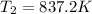
b)
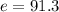 %
%
Step-by-step explanation:
A) First, let's write the energy balance:
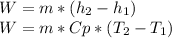 (The enthalpy of an ideal gas is just function of the temperature, not the pressure).
(The enthalpy of an ideal gas is just function of the temperature, not the pressure).
The Cp of air is: 1.004
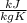 And its specific R constant is 0.287
And its specific R constant is 0.287
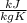 .
.
The only unknown from the energy balance is
 , so it is possible to calculate it. The power must be negative because the work is done by the fluid, so the energy is going out from it.
, so it is possible to calculate it. The power must be negative because the work is done by the fluid, so the energy is going out from it.
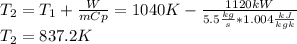
B) The isentropic efficiency (e) is defined as:
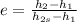
Where
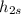 is the isentropic enthalpy at the exit of the turbine for the isentropic process. The only missing in the last equation is that variable, because
is the isentropic enthalpy at the exit of the turbine for the isentropic process. The only missing in the last equation is that variable, because
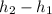 can be obtained from the energy balance
can be obtained from the energy balance
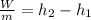
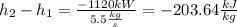
An entropy change for an ideal gas with constant Cp is given by:
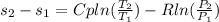
You can review its deduction on van Wylen 6 Edition, section 8.10.
For the isentropic process the equation is:
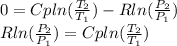
Applying logarithm properties:
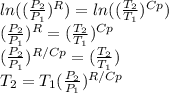
Then,
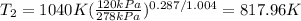
So, now it is possible to calculate
 :
:
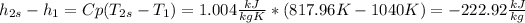
Finally, the efficiency can be calculated:
 %
%