Question

Find the 6th term of the geometric sequence whose common ratio is 3/2 and whose first term is 6.

Answer 1

The 6th term will be:

`a_6=(729)/(16)`

Explanation:

Given

• a₁ = 6

• common ratio r = 3/2

To determine

a₆ = ?

A geometric sequence has a constant ratio r and is defined by

`a_n=a_1\cdot r^(n-1)`

substituting a₁ = 6, r = 3/2

`a_n=6\cdot \left((3)/(2)\right)^(n-1)`

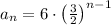
Determining 6th term

substituting n = 6 in the given equation

`a_n=6\cdot \left((3)/(2)\right)^(n-1)`

`a_6=6\cdot \left((3)/(2)\right)^(6-1)`

`=6\cdot (3^5)/(2^5)`

`=(3^5\cdot \:6)/(2^5)`

`=(3^5\cdot \:2\cdot \:3)/(2^5)`

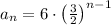
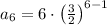
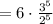
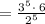
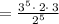
Cancel the common term

`=(3^6)/(2^4)`

`=(729)/(16)`

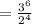
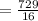
Therefore, the 6th term will be:

`a_6=(729)/(16)`