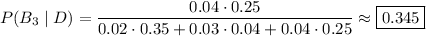I suppose the part about
"B1, B2, and B3, make 35%, 40%, and 25%"
should be taken to mean
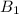 produces 35% of some product,
produces 35% of some product,
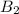 produces 40%, and
produces 40%, and
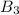 produces 25%. Then
produces 25%. Then
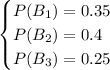
Each machine has some probability of making a defective product - denote this event by
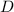 . Then
. Then

We want to find the probability that a defective product was made by machine
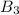 , i.e.
, i.e.
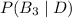 . By definition of conditional probability and the law of total probability, we have
. By definition of conditional probability and the law of total probability, we have
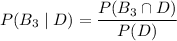
(def. of conditional probability)
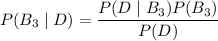
(def. of conditional probability)
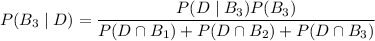
(law of total probability)
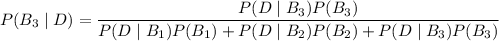
(def. of conditional probability; this result is also known as Bayes' theorem)
So we have