Question

A person standing at point C measures the angle of elevation to a point, A, at the top of a perpendicular cliff, to be 18°. After moving 2,200 feet directly toward the foot of the cliff, the person measures the angle of elevation to point A as 56°.

The height of the cliff is feet.

Answer 1

The height of the cliff is approximately 915 feet.

Explanation:

Refer to the diagram attached. Let B represent the point on the ground where the cliff measures an angle of elevation of 56°. Let AH be the height of triangle ABC on the base BC. H is on both line AH and line BC.

The three angles of triangle ABC will be:

• 
  `\rm \hat{A} = 18^(\circ)`;
• 
  `\rm A\hat{B}C = 180^(\circ) - 56^(\circ)`;
• 
  `\rm \hat{C} = 18^(\circ)`.

Only the length of segment BC is known. To find the height of the cliff, start by finding the length of segment AB. Apply the law of sine.

`\displaystyle \rm AB = BC*\frac{\sin{\hat{C}}}{\sin{\hat{A}}} = 2,200*\frac{\sin{18^(\circ)}}{\sin{38^(\circ)}} \approx 1.10* 10^(3) \; ft`.

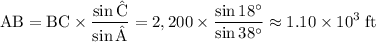In the triangle ABH,

• AB is the hypotenuse, and
• AH is the side opposite to the angle
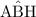  `\rm A\hat{B}H`.

`\rm AH = AB* \sin{A\hat{B}H} = 1.10* 10^(3) * \sin{56^(\circ)} \approx 915\; ft`.