Question

If the sum of the zereos of the quadratic polynomial is 3x^2-(3k-2)x-(k-6) is equal to the product of the zereos, then find k?

Answer 1

2

Explanation:

So I'm going to use vieta's formula.

Let u and v the zeros of the given quadratic in ax^2+bx+c form.

By vieta's formula:

1) u+v=-b/a

2) uv=c/a

We are also given not by the formula but by this problem:

3) u+v=uv

If we plug 1) and 2) into 3) we get:

-b/a=c/a

Multiply both sides by a:

-b=c

Here we have:

a=3

b=-(3k-2)

c=-(k-6)

So we are solving

-b=c for k:

3k-2=-(k-6)

Distribute:

3k-2=-k+6

Add k on both sides:

4k-2=6

Add 2 on both side:

4k=8

Divide both sides by 4:

k=2

Let's check:

`3x^2-(3k-2)x-(k-6) \text{ with }k=2`:

`3x^2-(3\cdot 2-2)x-(2-6)`

`3x^2-4x+4`

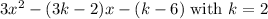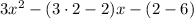
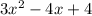
I'm going to solve
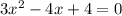`3x^2-4x+4=0` for x using the quadratic formula:

`(-b\pm √(b^2-4ac))/(2a)`

`(4\pm √((-4)^2-4(3)(4)))/(2(3))`

`(4\pm √(16-16(3)))/(6)`

`(4\pm √(16)√(1-(3)))/(6)`

`(4\pm 4√(-2))/(6)`

`(2\pm 2√(-2))/(3)`

`(2\pm 2i√(2))/(3)`

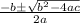
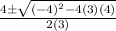
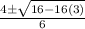
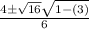
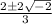
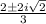
Let's see if uv=u+v holds.

`uv=(2+2i√(2))/(3) \cdot (2-2i√(2))/(3)`

Keep in mind you are multiplying conjugates:

`uv=(1)/(9)(4-4i^2(2))`

`uv=(1)/(9)(4+4(2))`

`uv=(12)/(9)=(4)/(3)`

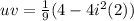
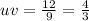
Let's see what u+v is now:

`u+v=(2+2i√(2))/(3)+(2-2i√(2))/(3)`

`u+v=(2)/(3)+(2)/(3)=(4)/(3)`

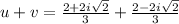
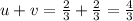
We have confirmed uv=u+v for k=2.