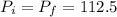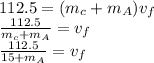Question

Suppose two astronauts on a spacewalk are floating motionless in space, 3.0 m apart. Astronaut B tosses a 15.0 kg IMAX camera to astronaut A. The IMAX camera is traveling with a speed of 7.5 m/s. What is the resulting speed of astronaut A after catching the camera?

Answer 1

`( 112.5)/(15+m_(A))=v_(f)`

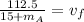
(we need the mass of the astronaut A)

Step-by-step explanation:

We can solve this by using the conservation law of the linear momentum P. First we need to represent every mass as a particle. Also we can simplify this system of particles by considering only the astronaut A with an initial speed
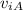`v_(iA)` of 0 m/s and a mass
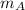`m_(A)` and the IMAX camera with an initial speed
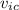`v_(ic)` of 7.5 m/s and a mass
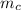`m_(c)` of 15.0 kg.

The law of conservation says that the linear momentum P (the sum of the products between all masses and its speeds) is constant in time. The equation for this is:

`P_(i)=p_(ic)+p_(iA)\\P_(i)=m_(c)v_(ic)+m_(A) v_(iA)\\P_(i)=15*7.5 + m_(A)*0\\P_(i)=112.5 (kg.m)/(s)`

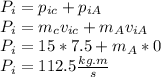
By the law of conservation we know that
`P_(i) =P_(f)`

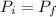
For
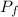`P_(f)` (final linear momentum) we need to treat the collision as a plastic one (the two particles stick together after the encounter).

So:

`P_(i) =P_(f)=112.5\\`

`112.5=(m_(c)+m_(A))v_(f)\\( 112.5)/(m_(c)+m_(A))=v_(f)\\( 112.5)/(15+m_(A))=v_(f)`