Question

Triangle $ABC$ has a right angle at $B$. Legs $\overline{AB}$ and $\overline{CB}$ are extended past point $B$ to points $D$ and $E$, respectively, such that $\angle EAC = \angle ACD = 90^\circ$. Prove that $EB \cdot BD = AB \cdot BC$.

Answer 1

Given :

ABC is a right triangle in which ∠ABC = 90°,

Also, Legs AB and CB are extended past point B to points D and E,

Such that,

`\angle EAC = \angle ACD = 90^(\circ)`

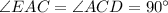
To prove :

`EB* BD=AB* BC`

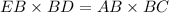
Proof :

In triangles AEC and EBA,

∠EAC= ∠ABE ( right angles )

∠CEA = ∠AEB ( common angles )

By AA similarity postulate,

`\triangle AEC \sim \triangle EBA`,

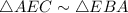Similarly,

`\triangle AEC \sim \triangle ABC`

`\implies\triangle EBA\sim \triangle ABC-----(1)`

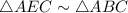
Now, In triangles ADC and CBD,

∠ACD = ∠CBD ( right angles )

∠ADC= ∠BDC ( common angles )

By AA similarity postulate,

`\triangle ADC \sim \triangle CBD`,

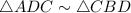Similarly,

`\triangle ADC \sim \triangle ABC`

`\implies \triangle CBD\sim \triangle ABC-----(2)`

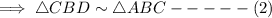
From equations (1) and (2),

`\triangle EBA\sim \triangle CBD`

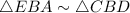
The corresponding sides of similar triangles are in same proportion,

`(EB)/(BC)=(AB)/(BD)`

`\implies EB* BD=AB* BC`

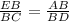
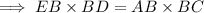
Hence, proved....