Question

25% of Netflix customers watch movies online from Netflix catalog. Assuming a binomial distribution, if a sample of 10 customers is selected, what is the probability that 3 or more but not greater than 7 watch movies online. Expert Ans

Answer 1

`\approx 0.47`

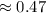
Explanation:

Let's define X = amount of customers that watch movies online. X has a binomial distribution with
`(1)/(4)` the probability of watching a movie online in a sample of 10 customers (we notate it as X
`\sim`B (10,
`(1)/(4)`), 10 and
`(1)/(4)` are the parameters of X).

Let's remember that the probability of getting exactly k successes (i.e. k customers that watch movies online) in n trials (n is the total of the sample), in a binomial distribution X with parameters (n, p), is given by the probability mass function:

`P (X = k) = \binom{n}{k} * p^k * (1-p) ^(n-k)`

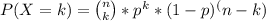
In our exercise, we need 3 or more but not greater than 7 successes. That means, we need to find out
`P(3\leq X\leq 7)`.

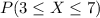Let's notice that this is equal to have 3, 4, 5, 6 or 7 customers that watch movies online.

So,
`P(3\leq X\leq 7) = P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7)`

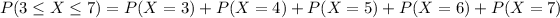
Now we just use the probability mass function, with n=10 and p=1/4, for each k ⊆ {3, 4, 5, 6, 7}:

`\binom{10}{3} * 1/4^3 * (1-1/4)^(10-3) + \binom{10}{4} * 1/4^4 * (1-1/4)^(10-4) + \binom{10}{5} * 1/4^5 * (1-1/4)^(10-5) + \binom{10}{6} * 1/4^6 * (1-1/4)^(10-6) + \binom{10}{7} * 1/4^7 * (1-1/4)^(10-7) =`

`\frac {10!} {3!7!} * 1/4^3 * 3/4^7 + \frac {10!} {4!6!} * 1/4^4 * 3/4^6 + \frac {10!} {5!5!} * 1/4^5 * 3/4^5 + \frac {10!} {6!4!} * 1/4^6 * 3/4^4 + \frac {10!} {7!3!} * 1/4^7 * 3/4^3 =`

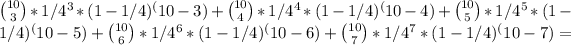
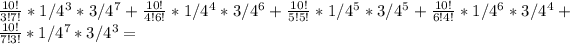
Now we just do the calculation and we get

`P(3\leq X\leq 7) \approx 0.47`