Question

What is the equation of the line?​

Answer 1

A line has an equation of a form,

`y=ax+b`

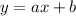
From a graph we can pick two points on the line, say A and B where,

`A(x_1,y_2),B(x_2,y_2)\longrightarrow A(0,0),B(1,-1)`

Using their coordinates we are able to calculate slope.

`a=\frac{\Delta{y}}{\Delta{x}}=(y_2-y_1)/(x_2-x_1)=(-1-0)/(1-0)=-1`

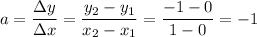
Hence,

`y=-1\cdot x+b`

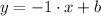
The x and y terms can be replaced with coordinates of one point either A or B. I'll pick A.

`0=-1\cdot0+b`

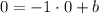
And now solve for b.

`0=0+b\Longrightarrow b=0`

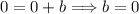
Hence,

`y=-1\cdot x+0`

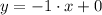
Simply,

`\boxed{y=-x}`

Hope this helps.

r3t40