Question

Which of the following statements best describes the graph of 3x – 2y = 4?

A) it is a straight line joining the points (6, 2), (5, 1), and (7,3).
B) lt is a straight line joining the points (0, -2), (2, 1), and (-2, -5).
C) It is a curve joining the points (3,-2), (2, 3), and (4. 1).
D) lt is a curve joining the points (0, 2), (-2, -1), and (4, 1).

Answer 1

B).

Explanation:

3x - 2y = 4 contains variables of degree one only, so this is a straight line.

Convert to slope-intercept form so it will be easier to check:

3x - 2y = 4

-2y = -3x + 4

y = 3/2 x - 2.

A). (6, 2): y = 3/2 *6 - 2 = 9-2 = 7 so its not A.

B). (0, -2): y = 0 - 2 = -2 so this fits.

(2, 1): y = 3/2 * 2 - 2 = 1 so this fits.

(-2, -5): y = 3/2*(-2) - 2 - -3-2 = -5 so this fits.

Answer 2

B

Explanation:

This is actually in the form of ax+by=c which is called standard form for a line.

I also know it is linear because the degree is 1. I know the degree is 1 because both variables are to the first power (you don't see this number because
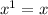`x^1=x` or
`y^1=y`).

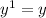So the choices are between A and B.

Let's see if it satisfies A:

Checking (6,2) for (x,y):

3 x - 2 y=4

3(6)-2(2)=4

18 - 4 =4

14 =4 is false so (6,2) is not on the given line.

Moving on to B:

Checking (0,-2) for (x,y):

3 x - 2 y=4

3(0)-2(-2)=4

0 + 4 =4

4 =4 is true so (0,-2) is on the given line.

Checking (2,1) for (x,y):

3 x - 2 y=4

3(2)-2(1)=4

6 - 2 =4

4 =4 is true so (2,1) is on the given line.

Checking (-2,-5) for (x,y):

3 x - 2 y=4

3(-2)-2(-5)=4

-6 + 10 =4

4 =4 is true so (-2,-5) is on the given line.

We have that all three pairs from choice B are contained on the line given.