Question

Adjust the window so you can find all of the points of intersection for the system of equations.

What are the roots of the original polynomial equation? Check all that apply.


–6


0


6


–4


3


8

Answer 1

6, -4, 3 for ed

Explanation:

Just did it

Answer 2

6,-4,3

Explanation:

We are given that a polynomial

`x^3+72=5x^+18x`

`x^3-5x^2-18x+72=0`

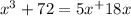
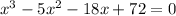
We have to find the original roots of polynomial equation

Substitute -6 in the polynomial

Then , we get

`(-6)^3-5(-6)^2-18(-6)+72`

`-216-180+108+72\\eq 0`

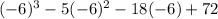
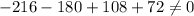
Therefore, it is not roots of the given polynomial.

Substitute x=0 then we get

`72\\eq 0`

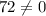
Hence, o is not a root of given polynomial.

Substitute x=6 then we get

`(6)^3-5(6)^2-18(6)+72`

`216-180-108+72=288-288=0`

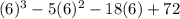
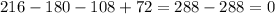
Hence, 6 is a root of given polynomial because it satisfied the given polynomial.

Substitute x=-4 then we get

`(-4)^3-5(-4)^2-18(-4)+72`

`-64-80+72+72=-144+144=0`

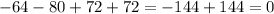
Hence, -4 is a root of given polynomial .

Substitute x=3 then we get

`(3)^3-5(3)^2-18(3)+72`

`27-45-54+72`

`99-99=0`

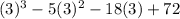
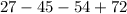
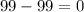
Hence, 3 is a root of given polynomial.

Substitute x=8 then we get

`(8)^3-5(8)^2-18(8)+72`

`512-320-144+72\\eq 0`

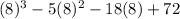
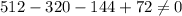
Hence, 8 is not a roots of given polynomial.